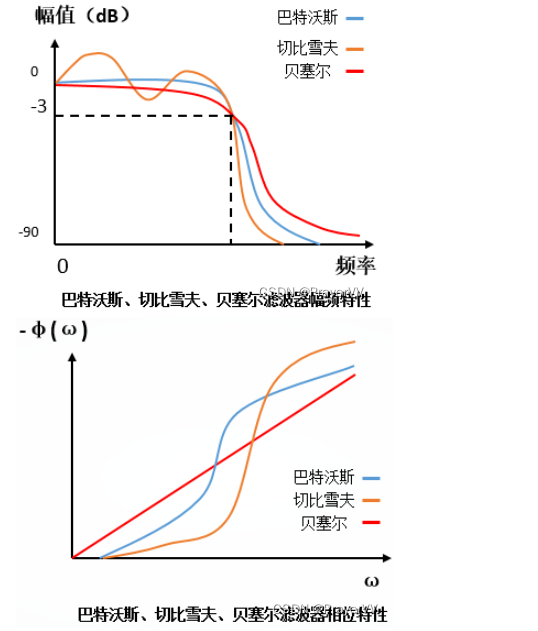
数字电子技术已无孔不入，然而我们仍身处于模拟的世界，原因显而易见。虽然数字的确可以用算法解决多种问题，但即使是的数字算法，在处理存在于模拟领域的现实世界实体时也有不足之处。这在要求高速度和高分辨率数据采集应用中尤其如此，如仪表、电机控制和数据采集系统。

对于希望捕捉和处理这种真实世界信号的设计者来说，问题是需要尽快进入数字域，而不损害这些信号信息。解决方案就在一个简单的平均算法（可减少噪声）和一个前端模拟低通滤波器 （LPF）。为了实现这些技术，器件要能提供高分辨率、高速度转换，并带有板载模拟和数字滤波才合适。

数字滤波器的种类

数字滤波器可以分为低通滤波器、带通滤波器、高通滤波器、带阻滤波器、椭圆滤波器、抽头滤波器、滤波器组等。

不同滤波器的特点

以下均收集于网络资料。

1.Gaussian

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

2.Bessel

贝赛尔滤波器是具有最大平坦的群延迟（线性相位响应）的线性过滤器。带通（通常为用户关注区域）的相位响应近乎呈线性。 Bessel滤波器可用于减少所有IIR滤波器固有的非线性相位失真。但它的选择性比同阶（或极数）的巴特沃斯（Butterworth）滤波器或切比雪夫（Chebyshev）滤波器要差。

3.Butterwroth

巴特沃斯滤波器也被称作最大平坦滤波器。巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有纹波，而在阻频带则逐渐下降为零。

4.Chebyshev

切比雪夫滤波器是在通带或阻带上频率响应幅度等波纹波动的滤波器。切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小，但是在通频带内存在幅度波动。

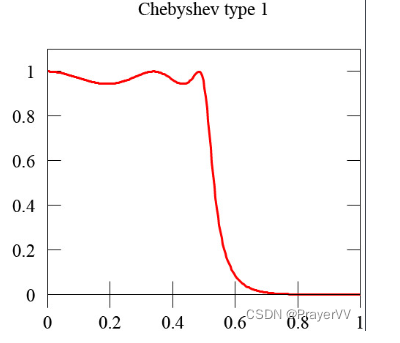
一型切比雪夫滤波器：

在通带（或称“通频带”）上频率响应幅度等波纹波动的滤波器称为“I型切比雪夫滤波器”。

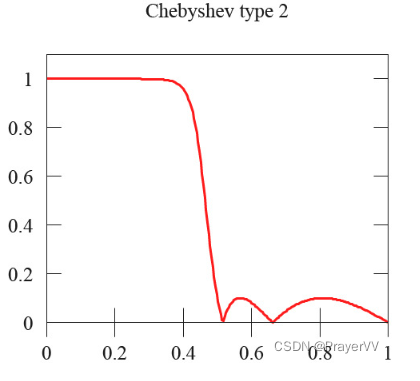
二型切比雪夫滤波器：

在阻带（或称“阻频带”）上频率响应幅度等波纹波动的滤波器称为“II型切比雪夫滤波器”。

5.Legendre

勒让德滤波器在通带内的波动优于切比雪夫I型滤波器。

6.Elliptic

椭圆滤波器是在通带和阻带等波纹的一种滤波器。椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下有着最小的通带和阻带波动。它在通带和阻带的波动相同，这一点区别于在通带和阻带都平坦的巴特沃斯滤波器，以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。从传递函数来看，巴特沃斯和切比雪夫滤波器的传递函数都是一个常数除以一个多项式， 为全极点网络， 仅在无限大阻带处衰减为无限大。 而椭圆函数滤波器在有限频率上既有零点又有极点。极零点在通带内产生等波纹， 阻带内的有限传输零点减少了过渡区， 可获得极为陡峭的衰减曲线。也就是说在阶数相同的条件下，椭圆滤波器相比于其他类型的滤波器，能获得更窄的过渡带宽和较小的阻带波动， 就这点而言， 椭圆滤波器是最优的。