
需要了解的是,损耗以半正弦波变化。 需要考虑从峰值到过零的变化,以得出器件的平均功耗。
IGBT 和二极管功耗计算
测量完这五个损耗分量后,需要将它们与测量条件相关联,以便计算每个芯片的总功耗。
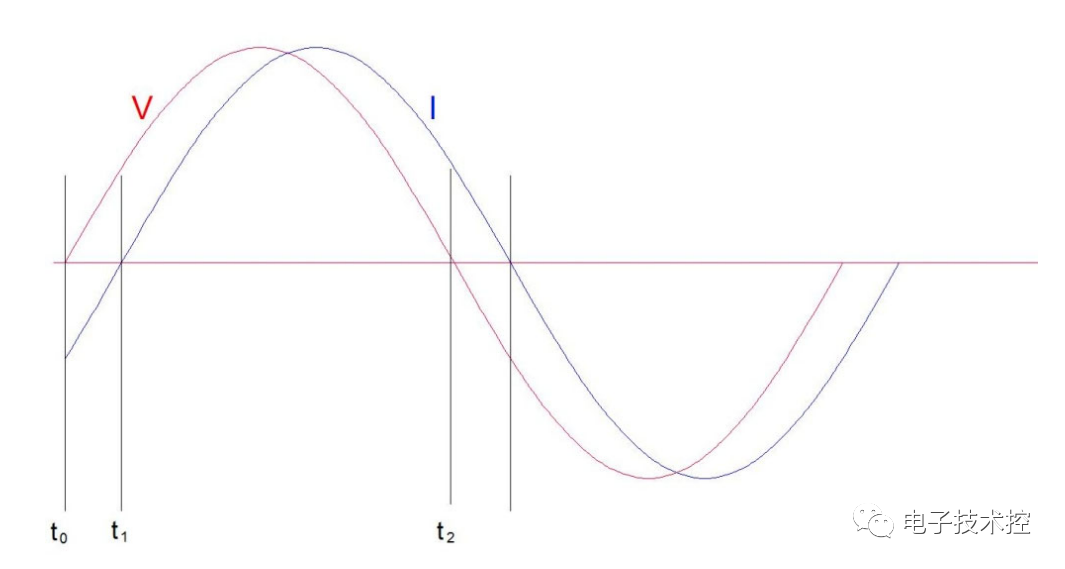
图 7. 感性负载波形
图 7 显示了感性负载(如电机)的典型电压和电流波形。
从 t0 到 t1,电流为电抗性,二极管传导电流。
从 t1 到 t2,电流为阻性,IGBT 传导电流。
这些时间段的功耗具有重要价值。 基于单个脉冲计算每个时间段的平均功耗非常复杂,但我们可以合理的精度进行估算。 为此,我们需要计算该时间段的平均功耗。
在这种情况下,有必要计算平均(或加热)当量。 对于电压和电流值,它是均方根值; 对于功率,它是平均值。
平均功耗
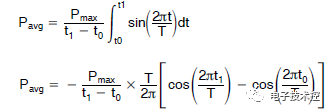
此公式计算的是正弦波每个四分之一部分的功率,因此要进行校正,我们需要在分母中添加一个因子 4。 只要电压过零点在 0° 和 90°之间(对于感性负载必定如此),这就是有效的,故公式变为:
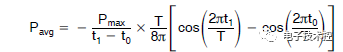
二极管
二极管在 t0 到 t1 期间传导电流。 利用电压过零点的波形可得出二极管的峰值功耗。 知道此功耗值后,我们可以使用 t0 到 t1 期间的平均功耗公式来求得二极管的平均功耗。
此时间段的示例计算如下所示。

2 W 功率出现在进入周期后的 2.5 ms 时。 要计算正弦波峰值处的等效功率,我们需要比较这两点的幅度。
峰值幅度出现在 90° 或 π/2 弧度处,相当于幅度 1。 2.5 ms 处的幅度为 sin(π × 2.5 ms/10 ms) 或 0.707,因此正弦波峰值处的功率为:
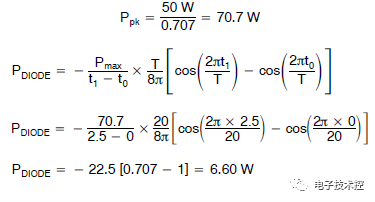
IGBT
对于正电压半周期,IGBT 在 t1 到 t2 期间传导电流。 IGBT 的平均功耗计算与二极管功耗的计算方法类似。 其示例计算如下所示。

对于 IGBT 分析,我们将计算完整半正弦波期间 (t0 – t2) 的 IGBT 功耗,然后计算二极管导通期间 (t0 – t1) 的 IGBT 功耗,再从前一功耗中减去后一功耗。 (责任编辑:admin) |

