在前面两篇文章中我们已经简单介绍了卡曼滤波以及所涉及的数学基础，今天让我们通过几个例子来进一步认识卡曼滤波器。

    现在我们准备好了第一个简单的例子，在本例中，我们估计静态系统的状态，静态系统是一个在合理时间段内不会改变其状态的系统，例如，一座塔可以是静态系统，状态可以是它的高度。

    在这个例子中，我们来估计金条的重量，假设我们的天平秤是无偏差的，即重量的测量没有系统误差，但测量可能包含随机噪声。

    在这个例子中，系统是金条，系统的状态是金条的重量，系统的动态模型是不变的，因为我们假设重量在短时间内不会改变。

为了估计系统的状态（即重量），我们可以进行多次测量并取其平均值

在第n时刻，估计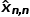

将是所有先前测量的平均值：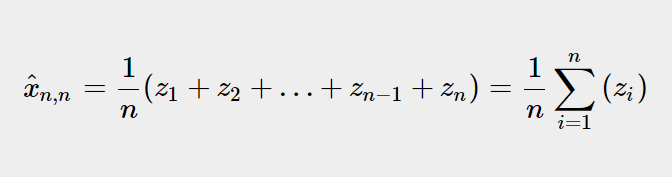

Example Notation:

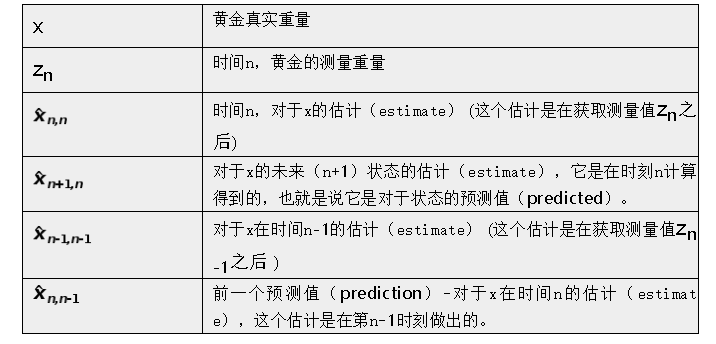注意: 变量上的插入符号（或帽子）表示估计值。

在本例中，因为系统是恒定不变的，所以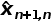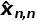

=

    尽管上面的等式在数学上是正确的，但在现实中并不适用，为了估计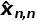

，我们需要记住所有的历史测量值；因此，我们需要一个大内存，如果我们想在每次新的测量后更新估计值，我们还需要重复计算平均值，因此，我们需要一个更强大的CPU。

    实际的做法是：仅保留最后的估计值（

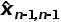） 并在每次获取新测量值后进行更新，我们可以用一个小小的数学技巧做到这一点：

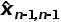是在n-1时刻对于x的估计，并且基于n-1时刻的测量值。

让我们基于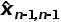

（对于x在时间n−1的估计)找到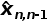

（对于x在时间n的预测值），换句话说，我们想根据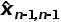

推断得到时间n的状态。

由于本例中的动态模型是静态的，即金条的重量不会随时间变化，因此x的预测状态等于x的估计状态：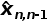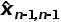

=

基于上述，当前状态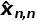

的估计值可以写为：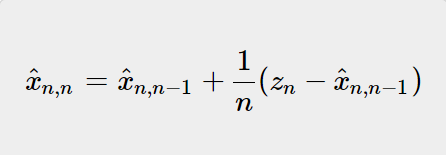

上述方程是五个卡尔曼滤波方程之一，它被称为状态更新方程。这意味着：

    因子1/n只适用于该示例，稍后我将讨论这个因素的重要作用，但现在，我先透漏个消息：在卡尔曼滤波器中，这个因素被称为卡尔曼增益，用Kn表示，下标n意味着卡尔曼增益可以随每次迭代而变化。

Kn的发现是鲁道夫·卡尔曼的重要贡献之一。

在我们深入卡尔曼滤波器之前，我们使用希腊字母αn代替Kn，因此，状态更新方程如下所示：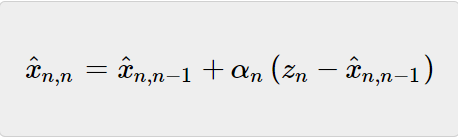

（Zn-Xn,n-1）项 代表“测量残差”，也称为革新，这项革新包含了新的信息。

    在本例中，1/n随着n的增加而减小，一开始，关于当前状态，我们没有足够的的信息；因此，第一次估计很大程度上是基于第一次测量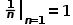

，随着我们继续，由于1/n减小，后续每个测量值在估计过程中的权重越来越小，在某个时刻，新测量的贡献将变得微不足道。

    让我们继续这个例子，在我们进行第一次测量之前，我们可以通过阅读金条上的印记来猜测（或粗略估计）金条的重量，这被称为初始猜测，这是我们的第一次估计。

这可能非常粗糙，但没关系，卡尔曼滤波器需要初始猜测作为预设。