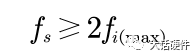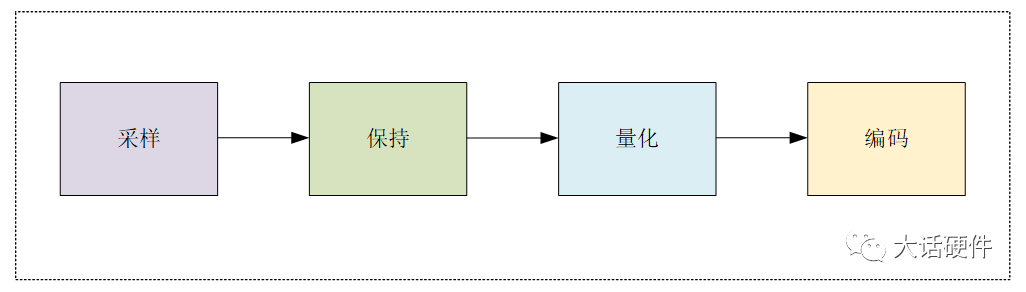
今天想给大家分析一下ADC的工作原理。

1. 模数转换

模数转换充当了模拟信号向数字信号的转换站，模拟信号因为容易受到干扰，信号处理时容易受到其他条件的限制，且不易存储的特点。在实际处理经常换成数字信号。在输出时，再又转换成模拟信号，典型的应用就是D类功放。

在ADC信号链中至少包括5个部分：前端传感器，信号调理，抗混叠滤波，输入防护，ADC。在模拟部分ADC是终端，在数字部分ADC是输入端，因此ADC是链接模拟和数字信号的核心模块。

2. ADC的工作原理

ADC完成了模拟信号向数字信号的转变，实现ADC转换的器件主要包括下面4个过程：采样——保持——量化——编码。

对应的电路如下所示：

目前市场上出现了很多类型的ADC，如果深入到ADC内部的细节看，采样和保持电路基本一样，但是在量化和编码方面却存在非常大的区别。正式这种区别 ，才产生了类似SAR，pipeline等之类不同的ADC架构。

2.1采样定理

模拟信号随时间连续变化，而数字信号是离散的，要得到转换后的数字信号第一步就是获取到模拟信号，即对模拟信号采样。因为数字信号无法做到随时间连续，所以只能间隔一定的时间对输入信号进行取样。在单位时间对模拟信号采样次数，被称为采样率，单位是Kmps。

根据香浓定理，为了能将取样信号还原成输入的信号则必须满足

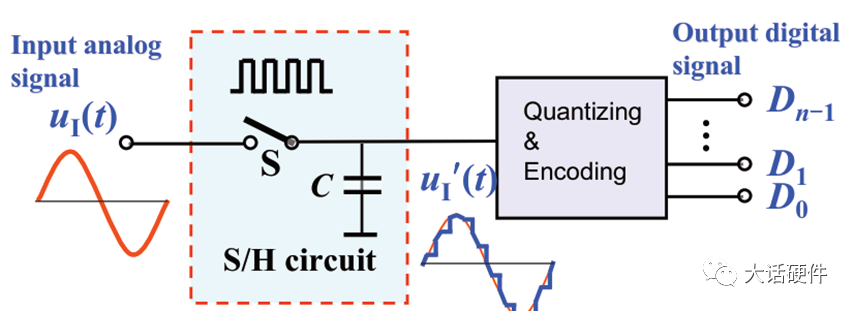
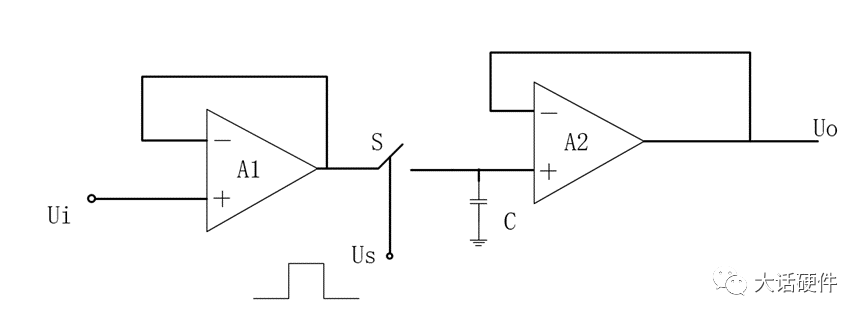
其中fs是取样频率，fimax是输入模拟信号的最高频率分量的频率。在实际的电路设计中，通常采样频率3~5倍的。

在采样的过程中，通常会涉及到两个定理容易被搞混淆，一个是香浓采样定理，另外一个是奈奎斯特采样定理。通常也成为奈奎斯特——香浓取样定理。可以查阅相关的资料学习。

2.2 S/H保持电路

保持电路的核心就是将采样后的模拟信号保持一段时间，在这段时间内信号要保持不变，能让后级的数字电路完成量化和编码。通常采用电容作为取样后的保持器件。原理如下所示：

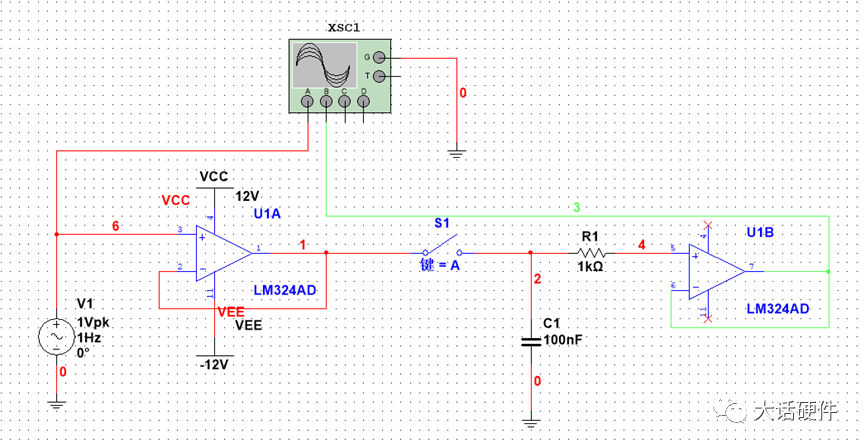
图中的电容C即为保持电容。采样开关和保持电容通常作为一个整体，成为S/H电路。A1和A2是两个运放，接成跟随的形式。这两个运放在IC里面是真实存在的，A1是用来隔离前面的信号，同时利用正向输入电阻无穷大的特性。A2是用来隔离后面的信号，利用输出阻抗在20~50Ω的特性。两边都是运放，把S/H电路夹在中间，可以降低噪声。

根据前面采样和保持电路的原理，可以对前两个过程进行仿真。

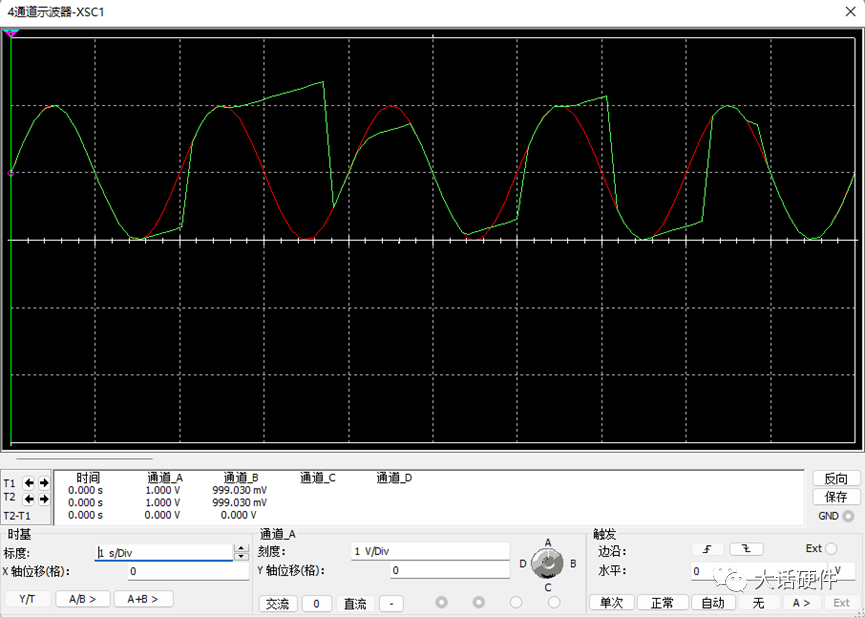
假设现在采样的速率比较低，手动就可以满足条件，从下面的波形可以看出，红色是原始波形，蓝色是采样到的信号，存在较大的失真，也就是无法正常还原采样的信号。

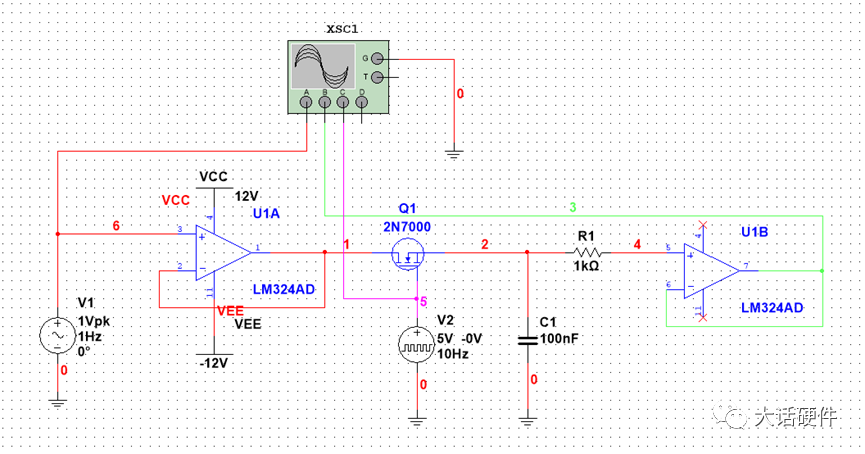
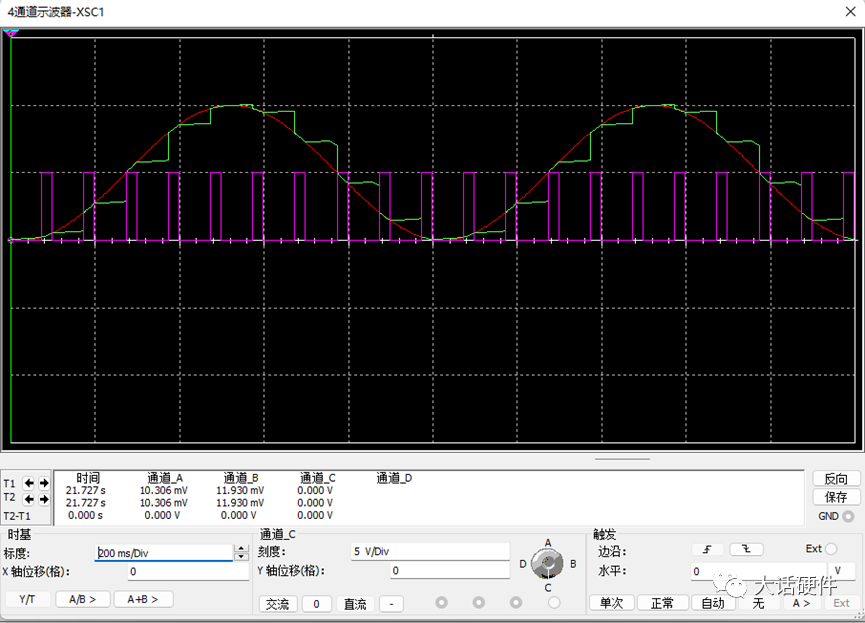
使用MOS管代替开关后，加入采样的驱动频率，仿真的结果可以看出，红色波形是输入信号，蓝色是采样后的信号，基本上能将输入信号进行还原。

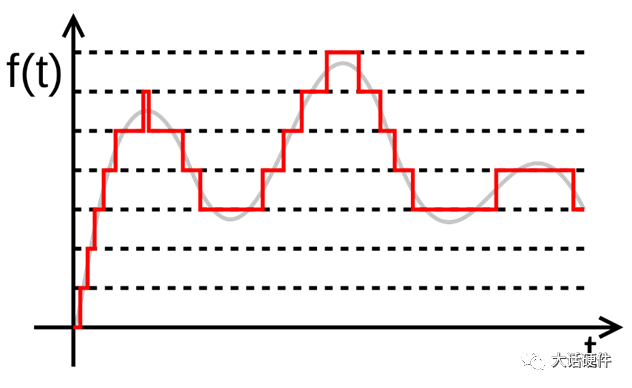
2.3 量化

量化是指将连续的模拟信号用有限个离散的数字信号近似化，量化后的模拟信号被划分为有限个且具有相同幅度的阶距的集合，如下图所示。                       

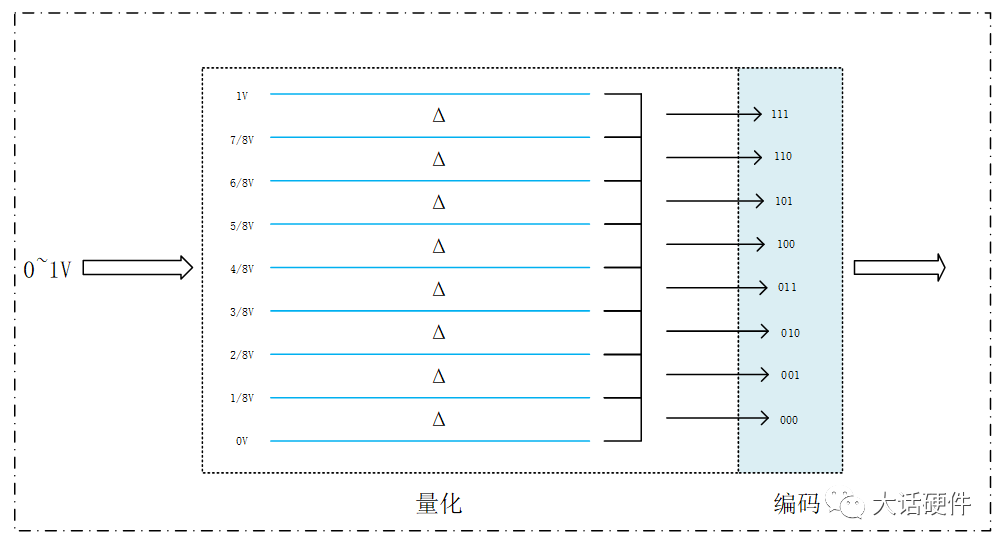
原始的模拟信号是连续无限的，用来量化的数字信号是离散有限的，那么在量化的过程中，会因为阶距的数量有限，部分模拟信号会被同一个量化后的值代替。从上图也可以看出，当离散后的数字信号为某一定值是，此时的模拟信号是在连续变化，因此，被量化的原始信号和量化后的信号之间存在差值，这种差值就是量化误差。

根据量化误差的定义可知，假如我们用无穷多个离散值来量化模拟信号，则每个阶距就是一个点，那么和原始信号几乎就是一样，没有量化误差，但实际并不可能存在，所以量化误差存在的根本原因是量化时的所使用的分辨率是有限的。

分辩率（Resolution）和精度经常被混淆。在初中物理我们学过，分辨率是用来描述刻度划分，精度是用来描述准确度。比如我们有两个把直尺，都是10cm，一把直尺上面有100个小刻度，另外一把直尺上有10个刻度，那么前者的分辨率是1mm，后者的分辨率是1cm。显然前者的分辨率要比后者高。在ADC中刻度的划分使用数字信号的位数来表示，比如理想的8位ADC分辨率就不如18位的ADC。

精度表示测量值和真实值之间的误差，或者说测量值偏离真值的幅度。使用两个相同分辨率的ADC来测量同一个模拟量，测出的结果也不可能完全相同，在不考虑量化误差的前提下，ADC本身会由于器件材料和工艺制程的影响，导致测量值偏离真实值。为了描述这种精度的大小，较长使用的是绝对精度和相对精度。绝对精度：用电压分辨率(LSB)的倍数表示，如 ± 1/1LSB 、± 1LSB 等。相对精度 ：用绝对精度除以满量程值的百分数表示 。

量化编码的不同导致不同ADC的类型。

2.4 编码

编码是ADC内部转换的最后一个过程，将量化后的结果，用二进制或者其他进制的形式表示出来，就是编码的过程。经过编码后，原始的模拟信号成为了数字信号。编码的本质是输出一串数字代码，这个代码会尽可能的接近当前采样到的模拟值。因此，使用哪种方式进行量化，将决定编码的规则。

现在有一个3位的ADC，对输入0~1V的电压进行量化编码，其过程如下。

3位ADC则可以将输入信号进行8等阶距的量化。                         

从量化的过程可以看出，当输入的电压在0~1/8V之间的任意一个模拟值时，此时输出的编码均是000，在1/8~2/8V之间的任意电压时，此时输出编码值均为001。那么这个量化过程引入最大的量化误差为1/8V，也就是量化时等阶距的值，一个1LSB。随着分辨率的增加，可以将模拟量量化为多位，因此分辨率增加，量化误差可以减少。

随着数字电路的发展，ADC其实大多数人用的越来越少，并不是因为ADC不用了，而是上游的芯片公司把ADC做到了芯片里面，直接以数字信号进行输出。但是无论是分离式的信号链，还是集成在芯片内部，ADC的整体框架没有变。

审核编辑：汤梓红