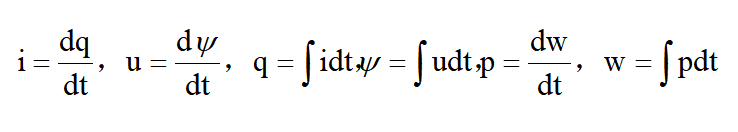(一)学习模拟电路，为何要学习电路数学基础呢？

如何高效学习电路数学？

我们知道，电路分析理论中关心的6个基本电路变量，是电压、电流、电荷、磁链、功和能，这6个量之间的数学关系为：

容易看到，它们之间的关系是用微积分描述的。所以，没有微积分，就没有电路分析理论。

电路中的参量有一个共同特征：它们幅值不仅随时间而变化，同时幅值又随频率而变化。我们把前者叫做时域变化，后者叫做频域变化。

在求微分方程时，我们发现直接求解很麻烦，但把它变换到复数空间中，微分方程变成代数形式。如此一来，极大地降低了分析难度。这种操作叫做拉普拉斯变换。如果要明白拉普拉斯变换的来龙去脉，就需要学习傅里叶级数和傅里叶变换。

同时我们还要学习正弦稳态电路的相量分析法，它的数学基础是《复变函数》，也即在复平面下的高等数学，显然，这也是以微积分为基础的。同时还要学习时域下信号的分解，冲激和卷积积分，这也是以微积分为基础的。

电路分析的数学基础非常广泛的，如微积分、傅里叶级数、傅里叶变换、拉普拉斯变换、卷积。

对于跨专业的硬件工程师而言，估计很难纯粹的去学习数学，更高效的是把它作为一种普通的运算在实际问题中加以应用。如同很多人为高效学习C语言，把C语言和单片机结合一起来学习。同样把电路数学基础与电路分析原理结合起来来学习不为一种高效的学习方法。

(二)学习模拟电路难点在哪里？

模拟电路的分析方法有哪些？

对于硬件电路来说，我们面对的电路主要可以分为两种类型。

第一种是有限输出状态类型，对于这种类型的电路，给定一个输入，它会产生一个输出，但这个输出处于一种比较粗糙的状态。

比如比较器，随着输入电压的高低，输出会产生一个被认为是“0”或“1”的输出，而代表“0”或“1”的电压会随不同的数字电路类型有所区别，但不论是哪种数字电路，对代表“0”或“1”的电压都不会是一个精确的值，而会是一个比较宽的范围。

再比如将三极管用做开关的电路，给定一个输入电压，三极管可能导通也可能截止，流过的电流在设计正确的情况下，通常由外部负载所决定，而不会由输入的电压决定。对于这样的电路，通常我们只需要简单的分析就会得到输出，也不会出现太多的意外情况，比如对于比较器来说，输出一个“0.5”或者对于三极管来说处于放大的状态。

对于这种开环类型的电路，给定输入，输出是有限的可预期的状态中的一种，在比较低的频率下，简单的以示波器上随时间变化的波形为基础进行时域分析通常就足够了。

第二种是输出连续变化的类型电路，它可以是复杂些的闭环状态的电路，也可以是简单些的RC或者RLC电路。通常会要求输出会随输入连续变化，且是一个可预期的、满足一定精度要求的、稳定的响应。这个时候简单的时域分析已不能满足我们分析电路的要求。我们要进入另一个角度来分析电路，也就是频域。对于绝大部分硬件电路工程师来说，其实都无法避免第二种类型的电路，也在不知不觉中进行一些必要的频域的分析。

第二种类型的电路就是我们常说的模拟电路。对于模拟电路来说，它的难点一个是对各种电子元器件纷繁复杂特性的学习与掌握，另一个是对分析模拟电路的方法进行学习掌握。有了这两个基础以后才有可能真正的进入模拟世界，进行模拟电路的设计，而不是处于一种雾里看花，懵懵懂懂的状态。

模拟电路涉及到的分析方法，其实有一套完整的理论基础进行支撑，LTI系统、卷积、傅里叶变换、拉普拉斯变换、传递函数、时域分析、频率响应、稳定性分析、频域补偿等等。我们这一次的课程，则是针对模拟电路的分析方法，以掌握必要的时域分方法和频域分析方法为目的。但又不仅仅直接局限于这两个明确的目标，而是把隐藏这两个分析方法背后的更多的内容讲出来，让学员更好的认识所面对的电路，让学员能够在模拟电路里走的更远。

编辑：黄飞